Penrose Tiling
November 23, 2025
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles- a remarkable mathematical discovery that tiles the plane infinitely without ever repeating, exhibiting perfect local order yet global irregularity.
Tiling the Plane
Tiling the plane means covering the entire two-dimensional Euclidean space \(\mathbb{R}^2\) with shapes called tiles without leaving any gaps or overlaps. A tiling uses one or more prototiles- basic (atomic) shapes that repeat according to specific rules.
The fundamental question: can we cover an infinite plane with a finite set of tile shapes? If so, what patterns emerge, and what symmetries do they possess?
Periodic Tiling and Symmetry
A periodic tiling repeats itself at regular intervals when shifted by a certain distance in one or more directions without rotation or reflection. This is translational symmetry. An example with 2 prototiles is shown below.

Periodic tiling using two rhombus prototiles. Source: Wikipedia - Penrose Tiling
Using only a single regular polygon, three tilings are possible: squares, equilateral triangles, and regular hexagons. These are the only regular polygons that tile the plane periodically when used alone. This is shown in the Figure below.
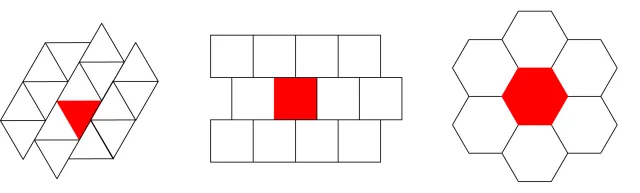
The three regular polygons that tile the plane. Source: Graham Shaw Cross
Aperiodic Tiling
An aperiodic tiling doesn't show translational symmetry entirely. No matter which direction you shift the pattern, it never perfectly repeats. Yet it fills the plane completely with no gaps or overlaps.
Before Penrose, mathematicians knew that aperiodic tilings existed. However, these were arbitrary constructions. The big question was- whether a set of tiles that can only tile the plane non-periodically, with no periodic arrangements possible.
The Problem Penrose Solved
In 1974, Roger Penrose discovered sets of tiles that admit only aperiodic tilings. His original set used six tiles, later reduced to just two: kites and darts (or thick and thin rhombi).
This solved a fundamental problem: by proving that aperiodicity can be forced by the tiles and not just by construction. Penrose tiles cannot form periodic patterns as they are inherently aperiodic. This was a breakthrough in mathematical tiling theory.
What Makes Penrose Tiling Special
Penrose tilings show local fivefold rotational symmetry- this was something that was thought to be impossible in tilings! Although, around certain points, the pattern displays perfect 5-fold rotational symmetry, but globally the tiling never repeats.
This paradox- local order without global periodicity- makes Penrose tilings unique. They possess long-range order and self-similarity at multiple scales, properties that connect them to quasicrystals discovered in physics decades later (for which Dan Shechtman got the Nobel Prize in Chemistry in 2011) .
The Mathematics in Euclidean Space
In \(\mathbb{R}^2\), Penrose tilings are constructed from two prototiles related by the golden ratio \(\varphi = \frac{1 + \sqrt{5}}{2} \approx 1.618\). The kite and dart have edge lengths and angles determined by \(\varphi\), ensuring they fit together only in specific, non-periodic ways.
The ratio of long side lengths to short sides in both tiles is \(\varphi:1\). A kite decomposes into two kites and two half-darts, while a dart decomposes into one kite and two half-darts.
References
- Aperiodic tilings: chiark.greenend.org.uk
- Github: apaleyes's code